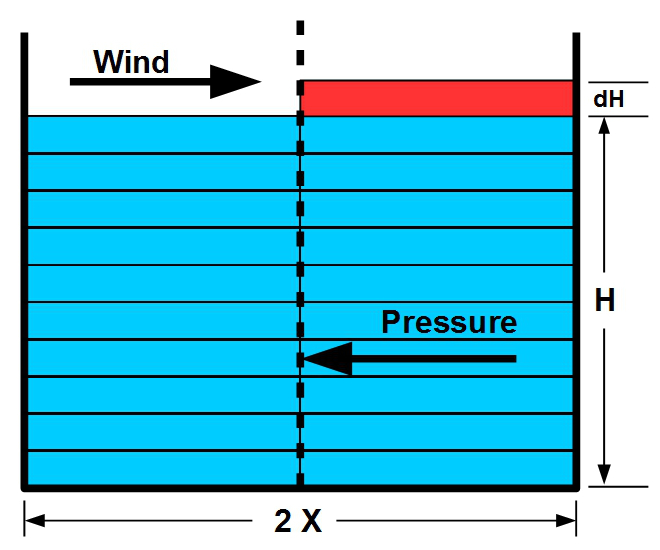
Figure 1. Pressure diagram of storm surge.
Why does shallow water surge and deep water does not? There is a differential equation that describes the balance of wind and hydraulic forces when strong winds blow across water. I present it here for the edification of any readers of my book Between Migdol and the Sea who are interested in the math behind Exodus 14.

Figure 1. Pressure diagram of storm surge.
Consider a tank of water diagrammed in Figure 1 (right). There is a porous divider down the middle of the tank which allows water to pass freely between left and right. The ten vertical levels are simply for calculating; there are no physical horizontal dividers. When no wind is blowing, we have the water level marked in blue. The pressure from the right and left sides balances at the middle, and the surface of the water is level. Simple enough.
When a strong wind blows from the left, it pushes water into the right side of the tank, thereby piling up water in the red cell. But the water doesn't pile up very high, and for this reason we can draw rectangles instead of diagonal lines. The red cell represents an incremental change in water level. If we let the system achieve a steady state, the pressure on the right and left sides of the tank will again balance. The water surface will acquire a low-angle tilt shown by the red cell.
What is that balance in mathematical terms? Since Figure 1 is a cross section, a real physical tank of water would have a Y-dimension extending into the page. I'll include that dimension so that the units work out correctly (but the Y-dimension will cancel out). We already know that the pressure of just the blue cells across the porous divider is equal, so we only have to calculate the pressure exerted by the red cell pressing down on the blue column.
Let Fwind be the force of the wind exerted on the water surface, measured in Newtons per square meter. The top of the entire tank measures 2 X by Y, and the top of the left column measures X by Y. So the wind force acting on the left side is:
Force of wind = Fwind * X * Y; N/m2 * m * m = Newtons
The red cell is held in place by the wind. But the red cell also weighs on every blue cell below it in the water column. Remember that water pressure is equal to the weight of the water column alone; X is not involved here. For each level in H, the pressure is unbalanced by the weight of the red cell at the top. What is the pressure exerted at the bottom of the red cell? Let g be the force of gravity and rho be the density of water. The height of the water column (dH) determines the pressure per square meter:
Pressure of red cell = dH * g * rho; m * m/sec2 * kg/m3 = N/m2
The force acting from right to left on the central divider at each level is:
Force of water at each cell = pressure * surface area at divider Force per cell = dH * g * rho * dH * Y; N/m2 * m * m = Newtons
The number of blue cells is equal to H / dH, where dH is the (small) height of each calculating level (blue and red). The total pressure balance in the entire tank is:
Force of wind = Force per cell * number of blue cells (H / dH) Fwind * X * Y = dH * g * rho * dH * Y * H / dH; Newtons
or simplified:
Fwind * X = g * rho * H * dH; Newtons (1)
If Fwind and X are held constant, and H (the depth of water) increases, then dH must decrease in order to maintain the equality and the balance of forces in the tank. Therefore deeper water will acquire a smaller angle of tilt when the wind blows. Shallow water surges more. Quod Erat Demonstrandum.
Now let's fiddle with the left side of the equation. X represents the fetch distance, the length of water along which the wind blows. Suppose X increases and H remains constant; our tank of water then represents a long inlet such as Long Island Sound. Equation (1) also states that the surge height dh will be large for Long Island Sound, and this result is exactly what was observed at Kings Point during Hurricane Sandy 2012.
And that is why the Gulf of Aqaba does not surge (and setdown) nearly as much as the Gulf of Suez. The Gulf of Suez is shallow. Equation (1) describes in mathematical terms why Moses and the Israelites did not cross the Red Sea at the Gulf of Aqaba.
Students of Calculus will recognize the notation dH as a differential, meaning that the quantity dH refers to a small change in the depth of water. Equation (1) uses the quantity X to refer to the length of the tank of water, from left to right. But X could also be a differential in Figure 1. Equation (2) below specifies a very narrow tank of water (narrow with respect to the depth of water H), but the balance of forces and units does not change.
Fwind * dX = g * rho * H * dH; Newtons (2)
Equation (2) relates small changes in the position dX to small changes in the water depth dH, also accounting for the total depth H and the constants Fwind, g, and rho. The marvelous thing about differential equations is that we can use them to calculate a smooth curve representing the water surface. None of this "piecewise linear" stuff here!
To solve differential equation (2), we integrate. Integration takes the differential equation and transforms it into a new equation that represents the entire water surface in terms of the variables X and H. The first step is to add integral signs before the variables, and place the constants out front:
Fwind * ∫ dX = g * rho * ∫ H * dH; Newtons (3)
Here comes the magical part. Remember your high school Calculus class? That integral sign means that you take the exponent, increase it by 1, and also multiply by the new exponent as a fraction, like this:
Fwind * X = g * rho * H2 / 2; Newtons (4)
I have set the constant of integration to zero for simplicity. The final step is to solve equation (4) for the depth (height) of water H in terms of the distance X from the left side of the tank (the origin).
H = √(2 * Fwind * X) / (g * rho); meters (5)

Figure 2. Water depth under strong wind stress.
Blue = Water depth calculated from differential equation (5).
Red = Water depth calculated from ROMS ocean model.
Click for larger image.
Aside from the constants, equation (5) says that the depth of water H increases according to the square root of the distance X from the left side of the tank. Let's plot that with some realistic values (Figure 2, right, in blue):
Note that the vertical scale of Figure 2 is greatly exaggerated. A human observer on the left would perceive the edge of a shallow lake, not a wall of water rising up in front of her.
As a check on the differential equation, I have also plotted in red the water surface calculated with the ROMS ocean model at a grid resolution of 100 meters (Figure 2). Yes, that red curve also looks like a square root. But something is wrong! The two surface profiles of Flat Lake do not match. What happened? The ocean model presumably has all the equations of fluid mechanics built into its Fortran code. Should not the analytical calculation match the ocean model? The numerical difference is small, but it's annoying.
With differential equations, it's all about the slope. The original differential equation (2) does not say anything about the absolute values of the plotted points, just about the shape of the curve. We could slide the entire blue curve in Figure 2 up and down and equation (2) would still remain true.
Remember that "constant of integration"? The value that I set to zero in equation (4) for simplicity? Yeah, that one. The constant of integration is used in Calculus theory and practice to adjust the overall height of the solved differential equation (5). By inspection of the numerical values in Figure 2 we can determine that the blue analytical curve needs a decrease of 0.1 meters (10 centimeters) in order to match the red curve calculated by the ROMS ocean model. Equation (5) becomes:
H = √(2 * Fwind * X) / (g * rho) - 0.1; meters (6)

Figure 3. Comparison of calculated surge heights.
Blue = Water depth calculated from differential equation (6),
including the constant of integration.
Red = Water depth calculated from ROMS ocean model.
Click for larger image.
Figure 3 (right) shows the results of the adjustment. The two lines are on top of each other, which is what we want. I really did plot both curves! You can see a tiny bit of red peeking out from under the blue curve at the left end of the plot (the origin).
ROMS is the Regional Ocean Modeling System. The water surface in Figures 2 and 3 approaches vertical as the depth nears zero meters, and the ROMS numerical model was not formulated to model near-vertical surfaces. Consequently, the discrepancy occurs at the near-vertical portion of the curve at the plot origin (left side). The remainder of the curves in Figure 3 are nearly identical.
Question: Which way should we have made the adjustment - to the analytical equation (5) or to the ocean model? If we constructed a 40-kilometer long Flat Lake uniformly 2 meters deep and somehow blew a strong wind across it for 12 hours, what would happen? Which configuration is closer to the Truth?
Answer: Probably the ROMS ocean model. Equation (5) depends on uniform wind stress across the entire water surface, and that's just not going to happen at the plot origin. A real wind is not going to blow as strongly down into that last centimeter where the water surface meets the ground, because of boundary effects. A real lake will not stack up quite vertically there, and the actual result will look more like the adjustment in Equation (6). I have personally spent many hours verifying that the ROMS ocean model does produce accurate heights for storm surge.
By the way: My book Between Migdol and the Sea contains NO derivations as complicated as this one. Chapter 8 calculates an estimate of the number of Israelites who took part in the Exodus using basic algebra.
Posted: August 12, 2015
Updated: August 12, 2015
Author: Copyright 2015 by Carl Drews.
Return to Migdol Book.